RÉCURSIVITÉ

RÉCURSIVITÉ

Les (semi-) fonctions récursives ont été introduites pour donner un équivalent mathématique à la notion métamathématique intuitive de (semi-) fonction effectivement ou mécaniquement calculable (cf. LOGIQUE MATHÉMATIQUE, chap. 4). Par souci de simplicité, nous considérons ici le cas des fonctions des entiers dans les entiers, bien que l’on puisse définir la notion de récursivité pour des fonctions des réels dans les réels, ou pour des fonctionnelles de type supérieur.

Dans la suite, N désigne l’ensemble des entiers naturels et on note ^(p) l’ensemble des applications de N^p dans N. Soit u 殮 N; on désigne par N l’ensemble N 聆u et par ^(p) l’ensemble des applications de N^p dans N. Si f 捻 ^(p) , on appelle domaine de f l’ensemble:

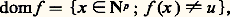et on dit que f n’est pas définie en x 捻 N^p si f (x ) = u . Ainsi, ^(p) se plonge dans ^(p) : un élément f de ^(p) appartient à ^(p) si et seulement si dom f = N^p .

L’ensemble des fonctions récursives à p arguments est un sous-ensemble dénombrable de ^(p) qui peut être défini de nombreuses façons différentes. Nous présenterons successivement un point de vue inspiré par l’informatique, une définition arithmétique et enfin une caractérisation de nature logique. Nous indiquerons ensuite quelques propriétés des éléments universels et de la complexité, notions qui s’introduisent de manière naturelle lorsqu’on adopte l’un ou l’autre de ces points de vue.

1. Définitions des fonctions récursives

Définition informatique

Nous donnerons cette définition de façon informelle, bien qu’elle puisse être présentée de façon rigoureuse dans le cadre de la théorie des automates.

On dispose de «boîtes» (ou registres de mémoire) dans lesquelles on peut enregistrer des nombres entiers naturels. Si n est le numéro d’une boîte, on désigne par 麗n 礪 le nombre qu’elle contient. On dispose également d’«instructions» à l’aide desquelles on établit des programmes, c’est-à-dire des suites finies d’instructions permettant de modifier les nombres contenus dans ces boîtes. Nous utiliserons des instructions d’un des quatre types suivants:

A(r ): augmenter de 1 le nombre contenu dans la boîte numérotée r et passer à l’instruction suivante du programme ;

D(r ): diminuer de 1 le nombre contenu dans la boîte numérotée r si 麗r 礪 礪 0, sinon ne rien faire, et passer à l’instruction suivante du programme;

E(r ⁱ , r ^j ): porter dans le registre r ⁱ le nombre contenu dans le registre r ^j et passer à l’instruction suivante;

T(q ⁱ , q ^j ) (r ) est l’instruction de transfert : Dans un programme, c’est-à-dire une suite finie d’instructions q ¹, q ², ..., q ⁱ , ..., q ^j , ..., q ⁿ ; lorsqu’on rencontre l’instruction T(q ⁱ , q ^j )(r ) on effectue l’instruction de nom q ⁱ si 麗r 礪 = 0, sinon on effectue l’instruction de nom q ^j .

Donnons un exemple de programme écrit avec le langage précédent:

Le lecteur vérifiera facilement que si x et y sont les nombres placés dans les registres 1 et 2 avant le début du calcul, les autres registres contenant 0, le programme s’arrêtera avec le nombre x + y dans le registre 1. Ainsi, ce programme permet d’effectuer l’addition de deux nombres; on le désigne par l’abréviation [1, 2] +[1] que l’on peut utiliser comme une nouvelle instruction (ou instruction de sous-programme) pour écrire de nouveaux programmes. On peut ainsi enrichir successivement le langage miniature dont nous sommes partis, mais il faut remarquer que les quatre types d’instructions élémentaires que nous avons introduits sont suffisants pour décrire n’importe quel calcul!

Notons qu’un programme peut ne pas s’arrêter pour certaines valeurs des arguments; par exemple, le programme suivant, composé d’une seule instruction q ¹: T(q ¹, q ¹)(1); en d’autres termes, ce programme calcule la semi-fonction u ^(p) de N^p dans N dont le domaine est vide.

On peut maintenant poser la définition suivante, calculatoire ou informatique, des semi-fonctions récursives.

Définition . Une fonction f 捻 ^(p) est dite calculable par programme , et on note f 捻 F size=1^戮(p) s’il existe un programme écrit à l’aide des quatre instructions ci-dessus et de l’instruction «arrêt» tel que, si x ¹, x ², ..., x ^p sont les nombres placés avant le début du calcul dans les registres 1 à p , les autres contenant 0, alors, si f (x ¹, ..., x ^p ) u , le programme s’arrêtera avec f (x ¹, ..., x ^p ) dans le registre 1 et, sinon (si f (x ¹, ..., x ^p ) = u ), il ne s’arrêtera pas.

Désignons par F size=1^戮 l’ensemble réunion des F size=1^戮(p) pour p 捻 N. On constate immédiatement un certain nombre de propriétés de clôture de cet ensemble; par exemple la somme, le produit... de deux fonctions calculables par programme l’est encore. En fait, F size=1^戮 est clos pour des procédés arithmétiques de définition très vastes, notamment la substitution, la récurrence et la minisation. Indiquons ces opérations qui nous conduiront à la définition arithmétique des fonctions récursives introduite simultanément par K. Gödel et J. Herbrand en 1931.

a ) La substitution S^{n m} est une application:

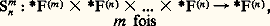définie par:

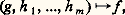où, pour tout x 捻 Nⁿ ,

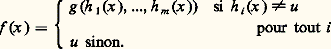b ) La récurrence Rⁿ est une application:

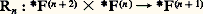définie par: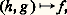

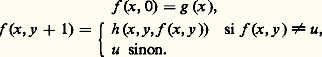où, pour tout x 捻 Nⁿ , y 捻 N,

c ) La minisation Mⁿ est une application: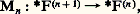

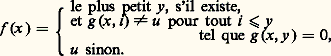soit g 料 f , où, pour tout x 捻 Nⁿ :

Il est facile de voir que F 戮 est clos pour ces différentes opérations. Par exemple, si g 捻 F size=1^戮(n+1) , montrons que f = Mⁿ (g ) appartient à F size=1^戮(n) . Il suffit de construire, à partir d’un programme de calcul de g , un programme de calcul de f . On vérifiera facilement que l’organigramme suivant, dans lequel le programme de calcul de g apparaît sous la forme abrégée d’une instruction de sous-programme, est celui d’un programme de calcul de f .

On démontre ainsi que F size=1^戮 contient l’ensemble ^R des semi-fonctions récursives que l’on va maintenant définir.

Définition arithmétique

Définition. L’ensemble ^R des semi-fonctions récursives est le plus petit ensemble de semi-fonctions contenant la fonction successeur, suc: NN, définie, pour tout x , par suc x = x + 1, les fonctions projections, pr^{i p} : N^pN, définies par pr^{i p} (x ¹, ..., x ^p ) = x ⁱ , les fonctions nulles, Z^p : N^pN, définies par Z^p (x ¹, ..., x ^p ) = 0, et qui est stable pour les opérations de substitution, récurrence et minisation.

On a vu que ^R 說 F size=1^戮. L’inclusion inverse est plus longue à établir, bien qu’elle ne présente pas de difficultés particulières.

Il suffit en effet d’«arithmétiser» le calcul par un programme pour s’en persuader. Une telle inclusion est généralement admise en vertu d’un énoncé périmathématique appelé «thèse de Church» suivant lequel toute semi-fonction mécaniquement calculable appartient à ^R. Cette «thèse», où la notion de semi-fonction mécaniquement calculable est prise en un sens intuitif, est justifiée par l’expérience: chaque fois que l’on a défini une classe de mécanismes de calcul, algorithmes de Markov, machines de Turing, systèmes de Post..., on a pu démontrer qu’ils définissaient des fonctions récursives. Il en est de même pour les fonctions calculables par programme (cf. aussi LOGIQUE MATHÉMATIQUE, chap. 4).

Définition logique

La définition arithmétique des fonctions récursives conduit à la définition logique.

Soit 硫 le langage de l’arithmétique, dont les symboles non logiques sont + pour désigner l’addition des entiers, 憐 pour la multiplication, 諒 pour l’ordre, = pour l’égalité; on ajoute, pour chaque entier n un symbole de constante n. Appelons formule de type une formule dans laquelle n’apparaît ni négation, ni implication, ni quantification universelle. La définition précise des formules de type est par induction; contentons-nous de cette définition intuitive qui signifie donc que l’on s’autorise comme seules opérations logiques la quantification existentielle, les quantifications universelles bornées, la conjonction et la disjonction pour écrire des formules d’arithmétique. Par exemple, si P(x ¹, x ², x ³) est un polynôme à coefficients dans Z, la formule suivante, à une variable libre x ³,

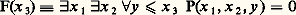est une formule de type du langage 硫.

Définition. Une application f 捻⁽ⁿ⁾ appartient à F size=1⁽ⁿ⁾ si et seulement si il existe une formule de type à n + 1 variables libres F(x ¹,x ², ..., x ⁿ , x ⁿ⁺¹ ) du langage 硫 telle que, pour tout système d’entiers a ¹, ..., a ⁿ , a ⁿ⁺¹ , on ait l’équivalence:

où N |= F(a¹, ..., aⁿ⁺¹ ) signifie que la formule sans variable libre F(a¹, ..., aⁿ⁺¹ ) est satisfaite dans la structure standard 麗N, +, 憐礪.

On a alors la proposition suivante: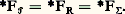

Il est facile en effet de vérifier que les fonctions qui interviennent dans la définition de ^R appartiennent à F size=1. Par exemple, la formule à p + 1 variables libres x ¹, x ², ..., x ^p+1 qui définit pr^{i p} est:

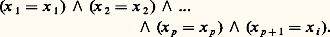On vérifie de même sans difficulté que F est stable pour les opérations de substitution et de minisation. La seule difficulté pour montrer que ^R 說 F size=1 est d’établir que F est clos par récurrence. La démonstration utilise la fonction 廓 de Gödel. C’est une fonction de type à trois arguments, qui est densifiante dans ^N, c’est-à-dire telle que, pour tout f 捻 ^N et pour tout p 捻 N, il existe n ¹, n ² 捻 N tels que, pour tout i 諒 p , on ait 廓(n ¹, n ², i ) = f (i ). On peut alors expliciter la récurrence par une formule de type , en remplaçant une quantification existentielle portant sur ^N par un quantificateur portant sur N² (existence d’un couple (n ¹, n ²) tel que...).

Pour se persuader de l’inclusion inverse F 說 ^R, on va introduire les notions d’ensembles récursifs et récursivement énumérables. Un ensemble X 說 N^p est dit récursif (on dit aussi décidable) si sa fonction caractéristique est récursive. Intuitivement, cela signifie qu’il existe un algorithme permettant de décider si un élément quelconque de N^p appartient ou non à X. Ainsi, les ensembles finis, l’ensemble des nombres premiers, l’ensemble des nombres qui sont somme de deux nombres premiers impairs... sont récursifs. Il est clair que les ensembles récursifs sont clos par union, intersection, passage au complémentaire et quantifications bornées. Un ensemble X 說 N^p est dit récursivement énumérable s’il est la projection d’un ensemble récursif Y de N^p+k . Par exemple, l’ensemble:

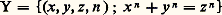est récursif, car, pour reconnaître (x , y , z , n ) 捻 Y, il suffit de calculer x ⁿ , y ⁿ et z ⁿ et de «tester» si x ⁿ + y ⁿ = z ⁿ .

Par contre, si:

cet ensemble X est récursivement énumérable d’après notre définition, mais on ignore actuellement si X est récursif. La fameuse conjecture de Fermat suivant laquelle X =1, 2 impliquerait si elle était vraie, que X soit récursif (cf. équations DIOPHANTIENNES, P. de FERMAT).

On peut donner d’autres définitions équivalentes des ensembles récursivement énumérables. En nous limitant au cas p = 1, il est par exemple équivalent de dire que X est récursivement énumérable ou que X = f (N), où f est une semi-fonction récursive dont le domaine est N, ou encore X = dom g , avec g 捻 ^R(1). Cette dernière caractérisation rend intuitive la notion d’ensemble récursivement énumérable: un ensemble X 說 N est récursivement énumérable (on dit aussi semi-décidable) s’il existe un algorithme qui s’arrête lorsqu’on l’applique à un élément x 捻 X et qui sinon ne s’arrête pas. Ces différentes caractérisations permettent de montrer facilement que les ensembles récursivement énumérables sont stables par réunion, intersection, quantifications bornées, quantification existentielle; mais on peut montrer que les ensembles récursivement énumérables ne sont pas stables par passage au complémentaire et qu’il existe des ensembles récursivement énumérables non récursifs.

Si on désigne par P^{(n) RE} l’ensemble des sous-ensembles récursivement énumérables de Nⁿ et par P size=1⁽ⁿ⁾ l’ensemble des sousensembles de Nⁿ qui sont définissables par une formule de type , il est facile de voir que P size=1⁽ⁿ⁾ 說 P^{(n) RE}; l’inclusion inverse P^{(n) RE} 說 P size=1⁽ⁿ⁾ est une conséquence immédiate de l’inclusion ^R 說 F size=1. Ainsi P^{(n) RE} = P⁽ⁿ⁾ size=1, ce qui entraîne F size=1 說 ^R, car f 捻 ^R si et seulement si son graphe est récursivement énumérable.

L’égalité P^RE = P size=1 est la caractérisation naturelle des ensembles récursivement énumérables: pour vérifier que X 捻 P^RE, il suffit d’en donner une définition arithmétique sans quantification universelle ni négation, ni implication, c’est-à-dire ne comportant que des conjonctions, disjonctions, quantifications existentielles ou projections, quantifications universelles bornées. Ce résultat admet un raffinement difficile à démontrer: on peut se passer des quantifications bornées pour définir les éléments de P^RE. Plus précisément, on dit qu’un sous-ensemble de N^p est polynomial si ses éléments sont les solutions d’un polynôme de p variables à coefficients dans Z, et qu’un sous-ensemble de N^k , k 捻 N, est diophantien si c’est la projection d’un ensemble polynomial de N^p+k . On a alors le théorème suivant.

Théorème de Matijasevi face="EU Caron" カ . Un ensemble X de N^k est récursivement énumérable si et seulement s’il est diophantien.

Comme corollaire de ce résultat, on peut affirmer l’existence d’un polynôme de plusieurs variables à coefficients dans Z dont l’ensemble des valeurs positives est l’ensemble des nombres premiers.

Ce résultat permet aussi de donner une réponse négative au dixième problème de Hilbert (cf. problèmes de HILBERT): Trouver un algorithme permettant de décider si un polynôme à coefficients dans Z admet des racines entières. Un tel agorithme n’existe pas car, si X 說 N est un ensemble récursivement énumérable non récursif, il existe, d’après le théorème de Matijasevi face="EU Caron" カ, un polynôme P(x , x ¹, x ², ..., x ^p ) tel que: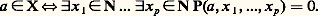

Si l’algorithme que recherchait Hilbert existait, il permettrait de décider, en l’appliquant au polynôme P(a , x ¹, ..., x ^p ) si a appartient à X ou non, ce qui est impossible puisque, par hypothèse, X est récursivement énumérable non récursif. Il n’est pas surprenant, compte tenu de la généralité de la question, que le dixième problème de Hilbert n’admette pas de solution. On pourrait limiter, par exemple, le nombre de variables et le degré, considérer seulement des polynômes homogènes, rechercher l’existence de solutions dans Q ou une extension algébrique de Q de degré fixé. Il existe de nombreux résultats techniques dans ces différentes directions, certains positifs, d’autres négatifs (cf. équations DIOPHANTIENNES, formes QUADRATIQUES). Indiquons ici seulement que les résultats négatifs permettent d’arriver à des définitions plus précises des ensembles récursivement énumérables (cf. Énumération universelle ).

2. Énumération universelle (principe du fonctionnement des ordinateurs)

Revenons à la définition informatique des fonctions récursives. L’alphabet que l’on utilise pour écrire des instructions, donc des programmes, est le suivant:

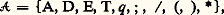si l’on convient d’écrire le nombre r avec r barres / et de séparer deux instructions par un astérisque. Par exemple, le programme:

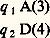sera écrit:

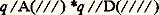dans cet alphabet.

Comme 遼 possède dix éléments, convenons d’utiliser les chiffres 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 au lieu des symboles A, D, E, T, q ,;, /, (,), respectivement. Le programme précédent s’écrit alors:

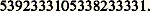Ainsi, si l’on convient d’utiliser la représentation décimale des nombres, un programme apparaît comme un nombre. Soit P 說 N l’ensemble des nombres dont l’écriture décimale correspond à l’écriture d’un programme. On peut vérifier que P est récursif. L’algorithme permettant de décider si x 捻 P ou x 殮 P consiste à faire l’analyse syntaxique de la représentation décimale de x , c’est-à-dire savoir si la suite correspondante de symboles est bien formée au sens de la grammaire de notre langage miniature de programmation.

Soit alors 﨏: N^R(p) l’application définie de la façon suivante:

– si x 捻 P, 﨏(x ) est la semi-application définie par le programme de numéro x (les arguments x ¹, ..., x ^p étant placés dans les registres 2 à p + 1 et le résultat pris dans le registre 1);

– si x 殮 P, alors 﨏(x ) = u ^(p) .

Soit maintenant 﨏 漣(x , x ¹, ..., x ^p ) = 﨏(x )(x ¹, ..., x ^p ). On se demande si 﨏 漣 appartient à ^R(p+1) . En d’autres termes, existe-t-il un algorithme permettant de calculer 﨏(x )(x ¹, ..., x ^p ) pour tout x , x ¹, ..., x ^p ? Un tel algorithme correspond au principe de fonctionnement des ordinateurs qui consiste à appliquer un programme quelconque x (enregistré en mémoire dans le registre 1) sur des arguments x ¹, ..., x ^p (enregistrés en mémoire dans les registres 2 à p + 1). Si on fait appel à la thèse de Church, on peut donc admettre que 﨏 漣 捻 ^R(p+1) . Signalons au passage que l’existence d’une énumération universelle récursive avait été trouvée par le logicien A. Turing avant la construction des ordinateurs.

L’application 﨏 possède de nombreuses propriétés et D. Lacombe en a fait une théorie générale abstraite. Mentionnons seulement deux propriétés élémentaires ayant des applications immédiates.

Existence d’une machine capable de se reproduire

Propriété a . Pour toute application 祥: N^R(p) telle que 祥 捻 ^R(p+1) , il existe a 捻 N tel que 祥(a ) = 﨏(a ).

Ainsi, par exemple, pour p = 1, si on prend 祥 = pr¹² définie par 祥(x , y ) = x pour tout x et tout y , il existe a 捻 N tel que, pour tout y 捻 N, on ait 﨏(a , y ) = 祥(a , y ) = a . Donc a est le numéro d’un programme qui, de par la définition même de 﨏, donnera a lorsqu’on l’applique sur un argument y quelconque. Donc a est le programme d’une machine qui se reproduit.

Indécidabilité de propriétés classiques

Propriété b . Pour tout ensemble non vide A 說 ^R(p) , l’ensemble 﨏^-1(A) est non récursif.

Ainsi, si on considère une propriété des fonctions calculables définissant un ensemble non vide A 說 ^R(p) , l’ensemble 﨏^-1(A) des programmes permettant de calculer (ou qui définissent) ces fonctions n’est pas récursif. Par exemple, pour p = 1, si:

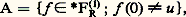﨏^-1(A) est l’ensemble des programmes qui s’arrêtent lorsqu’on les applique sur 0, et dire que 﨏^-1(A) est non récursif signifie qu’il n’existe pas d’algorithme général permettant de décider si un programme quelconque va s’arrêter lorsqu’on l’applique sur 0.

Le lecteur pourra, en choisissant des ensembles A 說 ^R(p) convenables, démontrer ainsi la non-existence d’algorithme pour des problèmes variés qui peuvent se poser en informatique (équivalence des programmes, problèmes divers d’arrêt, etc.).

Considérons donc les applications universelles 﨏: N^R(1) et 﨏 漣 捻 ^R(2). Par définition 﨏 est surjective, donc, pour tout ensemble X 說 N récursivement énumérable, il existe a 捻 N tel que X = dom 﨏 (a ), d’après la dernière caractérisation des ensembles récursivement énumérables. Soit alors W = dom 﨏 漣. D’après le théorème de Matijasevi face="EU Caron" カ, il existe un polynôme P(x , y , x ¹, ..., x ^k ) à coefficients dans Z tel que:

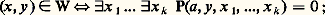pour cette raison, on appelle le polynôme P un polynôme universel.

I. V. Matijasevi face="EU Caron" カ et J. Robinson ont étudié ces polynômes universels et montré qu’il en existait un, U(a , y , x ¹, ..., x ¹³), avec k = 13. Ainsi, tout ensemble récursivement énumérable ou diophantien X 說 N peut être défini par une équation diophantienne en treize variables:

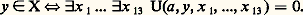On connaît certains couples ( 嗀, k ) pour lesquels il existe un polynôme universel de degré 嗀 avec k inconnues, par exemple les couples (4, 153), (6, 129), (20, 86), etc.; par ailleurs, des résultats d’arithmétique classique permettent d’affirmer que d’autres couples, par exemple (2, n ), n 捻 N, ne conviennent pas. La frontière entre le «décidable» et l’«indécidable» exprimée sous cette forme est encore mal connue et pose des problèmes difficiles d’arithmétique.

Pour terminer ce chapitre, nous donnerons deux illustrations des notions précédentes dans le cadre de la théorie élémentaire de la démonstration.

Considérons le langage de l’arithmétique qui a été introduit plus haut à l’occasion de la définition logique des ensembles récursivement énumérables et soit T un système d’axiomes dans ce langage permettant de démontrer les propriétés suivantes:

– la table positive de l’addition:

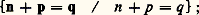– la table négative de l’addition:

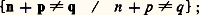– la table positive de la multiplication:

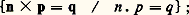– la table négative de la multiplication:

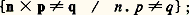et, pour tout entier n , les formules:

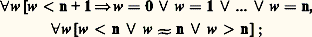on peut prendre pour T, dans ce cas on l’appellera ¹, la théorie dont les axiomes sont les formules précédentes.

Comme nous l’avons fait pour les programmes, on peut numéroter les formules à k variables libres du langage 硫; d’autre part, si F est une formule close, on définit la relation T 塞 F qui signifie que F est un théorème de la théorie T.

Considérons l’application:

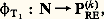définie par:

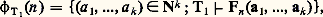où Fⁿ est la formule à k variables libres de numéro n du langage 硫 dans une bonne numération des formules. On démontre facilement que 﨏^T1 est une énumération universelle des sous-ensembles récursivement énumérables de N^k qui est récursivement isomorphe à l’application 﨏 du début de ce chapitre et possède donc exactement les mêmes propriétés. Ce résultat correspond à la partie élémentaire du premier théorème de Gödel. La seconde partie de ce théorème dit que la théorie ¹ est essentiellement indécidable, c’est-à-dire que toute théorie récursivement axiomatisable T qui contient ¹ n’est pas récursive; plus précisément, l’ensemble des théorèmes de T n’est pas récursif, à une bonne numérotation près des formules. Cela résulte du fait que les sous-ensembles de N fortement représentables dans ¹ sont les ensembles récursifs – on dit que X 說 N est fortement représentable s’il existe une formule F(x ) à une variable libre telle que:

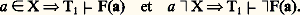Une seconde illustration des notions introduites ci-dessus est une forme du second théorème d’incomplétude de Gödel (cf. Indécidabilité et décidabilité pour d’autres formes). Ce résultat affirme qu’il existe une équation diophantienne n’admettant pas de racines dans N et dont on ne peut pas démontrer qu’elle est sans solution. Dans la formulation originale, on met en évidence une formule close Coh^T1 de l’arithmétique (qui exprime la cohérence de ¹) vraie dans N mais non démontrable dans ¹. Plus précisément, soit:

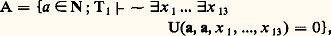où U(a , y , x ¹, ..., x ¹³) est le polynôme universel introduit ci-dessus. Alors A est récursivement énumérable car l’ensemble des théorèmes (c’est-à-dire des numéros des formules closes qui sont des théorèmes) de ¹ est récursivement énumérable. Par suite, il existe n 捻 N tel que:

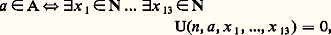donc: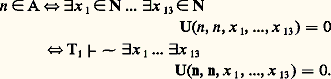

La dernière équivalence provient de la définition de l’ensemble A.

Si n 捻 A, nous avons une contradiction. En effet, si l’équation U(n , n , x ¹, ..., x ¹³) = 0 a une solution dans N, alors on démontre dans ¹ que:

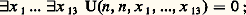ceci est un cas particulier du fait suivant, facile à vérifier par induction sur la longueur des formules, que, pour toute formule close de type , la vérité dans N est équivalente à la démontrabilité dans une théorie T cohérente contenant ¹ (bien entendu, cette propriété est fausse pour des formules quelconques, en particulier, comme on va le voir, pour les formules qui sont des négations de formules du type ).

Ainsi n 殮 A, donc l’équation U(n , n , x ¹, ..., x ¹³) = 0 n’a pas de solution dans N et on ne démontre pas dans ¹ la formule:

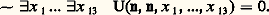On remarquera au passage que ce raisonnement est valable pour toute théorie cohérente T contenant ¹.

3. Complexité

Un programme de calcul x d’une semi-fonction récursive f = 﨏(x ) étant donné, où 﨏: N^R(1) est l’énumération universelle définie dans le chapitre précédent, on peut effectuer deux types de mesures. La première consiste, par exemple, à mesurer le nombre d’instructions d’un certain type de ce programme x . On définit ainsi une application m : NN en désignant par m (x ) le nombre d’instructions de ce type dans le programme de numéro x pour x 捻 P (et 0 sinon). Il est clair que m est une fonction récursive; dans ces conditions, il pourrait être intéressant de calculer l’application c : NN définie par

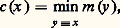où y 令 x signifie 﨏(y ) = 﨏(x ); ainsi, c (x ) est le nombre minimal d’instructions du type considéré pour calculer la semi-fonction définie par le programme de numéro x . Malheureusement, on déduit immédiatement de la propriété b du chapitre précédent, sous une hypothèse facile à vérifier pour toutes les pseudo-mesures m , que l’application c n’est pas calculable.

La seconde approche consiste à mesurer, par exemple, le nombre d’instructions, la quantité de mémoire, etc., utilisées par le programme de numéro x lorsqu’on l’applique sur l’argument y , en d’autres termes, faire une mesure sur le calcul lui-même.

On définit ainsi une application 祥: N^R(1), où 祥(x )(y ) est une certaine complexité du calcul du programme de numéro x lorsqu’on l’applique sur l’argument y . On constate que toutes les mesures qu’il est naturel de faire sur les calculs (temps, mémoire, etc.) correspondent à des applications 祥 qui possèdent les trois propriétés suivantes: 祥 捻 ^R(2); dom 祥 = 﨏; le graphe de 祥 est récursif.

Les complexités 祥 possédant ces trois propriétés n’interviennent pas seulement en informatique. Reprenant la première application du chapitre précédent, définissons 祥^T1: N^R(1) de la façon suivante:

On constate que 祥^T1 possède les trois propriétés relatives à l’énumération universelle 﨏^T1 des sous-ensembles récursivement énumérables de N et donc que 祥^T1 va posséder toutes les propriétés qui découlent de ces trois axiomes. On peut démontrer par exemple les deux propositions suivantes que nous énoncerons de façon informelle en utilisant le langage de l’informatique afin de les illustrer simplement.

Proposition . Soit 祥 une complexité et t 捻 ^R(1). Il existe f 捻 ^R(1) tel que, pour tout programme i permettant de calculer f , on a: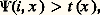

sauf pour un nombre fini de x .

En d’autres termes, il existe des fonctions dont tout calcul est aussi compliqué que l’on veut.

Proposition (théorème d’accélération de Blum). Soit g 捻 ^R(1); alors, pour toute mesure de complexité 祥, il existe f 捻 ^R(1) tel que:

a ) Pour tout programme i permettant de calculer f , on a:

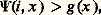sauf pour un nombre fini d’arguments x .

b ) Pour tout programme i permettant de calculer f , il existe un programme j de calcul de f tel que:

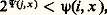sauf pour un nombre fini de x .

En d’autres termes, il existe f 捻 ^R(1) dont tout calcul est aussi compliqué que l’on veut (sauf pour un nombre fini d’arguments) et tel que, pour tout programme i , il en existe un autre j dont le calcul, sauf pour un nombre fini d’arguments, est beaucoup moins compliqué que le calcul par le programme i .

Ce dernier résultat est assez déroutant, dans la mesure où il montre l’existence de fonctions n’ayant pas de meilleur programme de calcul. Mais, bien entendu, toutes les fonctions ne possèdent pas la propriété de la fonction f du théorème et le problème de caractériser les fonctions «non accélérables» (pour différents sens de ce mot) reste ouvert. Certains progrès récents laissent supposer l’existence de solutions accessibles. Il en va de même pour les questions que soulève la première proposition dont la démonstration s’effectue par diagonalisation sur l’ensemble des fonctions «faciles» à calculer. On peut ainsi, par exemple, rechercher des propriétés arithmétiques, analytiques, etc., des fonctions caractéristiques des sous-ensembles récursifs de N qui impliqueraient une grande complexité de calcul. Les travaux dans ce domaine sont passablement techniques.

Indiquons simplement à ce propos quelques résultats sur les hiérarchies de fonctions récursives. Si f est une fonction récursive totale (c’est-à-dire dont le domaine est N), il se trouve que les trois notions de taux de croissance à l’infini, complexité de calcul de f et indépendance dans un sous-système de l’arithmétique d’une formule du type 葉x 說y f (x ) = y sont étroitement liées.

Précisément, définissons la hiérarchie suivante de fonctions indexée par des ordinaux:

Ainsi, f ¹(x ) = 2x , f ²(x ) = 2^x 練 x , etc.

Pour chaque n 捻 N, la fonction f ⁿ permet de définir un ensemble 劉ⁿ de fonctions récursives en prenant la clôture par rapport à certaines opérations que nous ne préciserons pas et on montre que 劉⁰ 說 劉¹ 說 劉² 說 ..., les inclusions étant strictes car f ⁿ⁺¹ croît beaucoup plus rapidement que toute fonction de 劉ⁿ .

On montre alors, si 祥 est la complexité qui mesure le nombre d’étapes de calcul dans tout modèle raisonnable d’ordinateur, comme celui utilisé ci-dessus pour la définition informatique des fonctions récursives, les machines de Turing, etc., que si R^f size=1^切 désigne l’ensemble des fonctions récursives pour lesquelles il existe un programme de calcul i tel que 祥(i , x ) 麗 f (x ) sauf pour un nombre fini d’entiers x , on a, pour n 礪 2:

où f ^{n (p)} = f ⁿ 獵 ... 獵 f ⁿ , p fois.

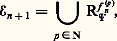Ainsi 劉³, qui est l’ensemble des fonctions élémentaires définies par L. Kalmar, est l’ensemble des fonctions récursives qui peuvent être calculées en un temps inférieur à f ^2(p) (x ) qui est de l’ordre de:

Il est donc clair qu’une fonction récursive f qui n’appartient pas à 劉³ n’est pas calculable pratiquement. En effet, si l’on admet que le temps minimal d’une étape de calcul est le temps mis par la lumière, à la vitesse de 300 000 km/s, pour franchir la longueur d’un proton, soit 10^-13 cm et que l’âge de l’Univers est d’environ 40 milliards d’années, alors le nombre d’étapes de calcul depuis le début des temps est de l’ordre de 2¹²⁸ ou encore 2^27.

L’étude des ensembles 劉⁰, 劉¹, 劉², 劉³ présente un intérêt du point de vue informatique puisque l’on peut, en première approximation, dire que ce sont les ensembles de fonctions pratiquement calculables. On rencontre à leur propos de nombreux résultats et problèmes, comme celui, par exemple, de caractériser l’ensemble 劉² des fonctions caractéristiques qui sont dans la classe 劉² et le fameux problème 戮 = N 戮, d’ailleurs lié au précédent, qui, s’il était résolu positivement, impliquerait, pour toute une série de problèmes combinatoires, l’existence d’algorithmes beaucoup plus rapides que ceux qui sont actuellement connus. Sans entrer dans le détail de ces études (hiérarchie de Stockmeyer, Wrathall, Cleave, etc.), disons simplement qu’une voie qui semble se dessiner pour les aborder serait, à la suite des travaux de Paris, l’étude fine des modèles non standards de fragments de l’arithmétique.

Donnons quelques résultats relatifs aux ensembles 劉ⁿ pour n 礪 3. On démontre les égalités suivantes: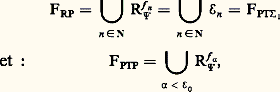

où ^RP est l’ensemble des fonctions récursives primitives (c’est-à-dire les fonctions que l’on obtient en supprimant le schéma de minisation dans la définition de ^R) et ^PTP (resp. ^PT size=1¹) l’ensemble des fonctions récursives dont on peut prouver dans l’arithmétique de Peano P (resp. dans l’arithmétique de Peano P ¹ obtenue à partir de P en limitant le schéma d’induction aux formules du type ) qu’elles sont totales au sens suivant: si F(x , y , z ) est la formule de type de l’arithmétique qui représente le graphe de l’énumération universelle 﨏 définie au chapitre précédent, on a:

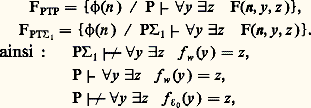où T 塞 / F signifie que F n’est pas un théorème de la théorie T. Ces théorèmes permettent de démontrer que certains résultats combinatoires vrais ne sont pas démontrables dans les sytèmes P, P ¹. Donnons deux exemples de tels résultats.

Considérons le problème suivant. Étant donné un nombre n , on écrit ce nombre en base 2, puis on soustrait 1, on change la base 2 en la base 3, on soustrait 1 à nouveau, etc. Soit g (n ) le plus petit entier m tel que la procédure précédente s’arrête avec 0 en m étapes. Du fait qu’il n’existe pas de suite infinie décroissante d’ordinaux, il est facile de voir que l’on définit bien ainsi une fonction g récursive. Kirby et Paris ont démontré que cette fonction g est équivalente du point de vue de la croissance à la fonction f ^w , introduite par Ackermann en 1940 comme exemple de fonction récursive qui n’est pas récursive primitive. Ainsi, on ne démontre pas dans le système P ¹:

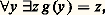tandis que cette propriété est démontrable dans l’arithmétique de Peano.

Si dans le processus précédent on avait décomposé n en base k pure, c’est-à-dire en n’utilisant que des chiffres inférieurs à k , notamment pour les exposants qui apparaissent dans la décomposition de n , la fonction h que l’on obtient (fonction de Goodstein) est équivalente du point de vue de la croissance à f size=1^劉0. Ainsi, on ne démontre pas dans l’arithmétique de Peano

bien que l’on montre, en utilisant une induction jusqu’à l’ordinal 劉⁰ que cet énoncé est vrai dans le modèle standard N.

De même, Paris et Harrington ont démontré qu’un certain énoncé combinatoire dérivé du théorème classique de Ramsey est vrai mais n’est pas démontrable dans l’arithmétique de Peano. En effet, pour tout n , k , il existe p tel que, si q 礪 p et si g est une application de l’ensemble [q ]^k des sous-ensembles à k éléments de0, 1, ..., q, à valeurs dans0, 1, ..., n, alors il existe un ensemble Y 說0, 1, ..., q, dont le nombre d’éléments est supérieur au minimum de Y et supérieur à k , tel que la restriction de g à [Y]^k soit constante.

Il s’agit là d’un énoncé combinatoire qui peut être explicité par une formule de l’arithmétique vraie dans N. Toutefois, si on considère la fonction R(n , k ) qui désigne le plus petit p dont l’existence est assurée par ce résultat, on constate que la fonction H(x ) = R(x , x ) est une fonction récursive équivalente du point de vue de la croissance à f size=1^劉0. Ainsi, dans l’arithmétique de Peano, on ne peut pas montrer l’énoncé: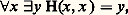

pourtant vrai dans le modèle standard N.

Récemment, on a démontré de cette façon (Friedman) l’indépendance d’énoncés combinatoires pour des théories beaucoup plus fortes que l’arithmétique de Peano.

4. Indécidabilité et décidabilité

L’étude de l’indécidabilité des théories mathématiques relève de la théorie des fonctions récursives en deux sens: en premier lieu, car un résultat d’indécidabilité signifie qu’une certaine fonction, à savoir la fonction caractéristique de l’ensemble des théorèmes (modulo une bonne numération des formules du langage de la théorie), n’est pas récursive, et, en second lieu, car l’indécidabilité d’une théorie mathématique se démontre la plupart du temps en utilisant le théorème de transfert de A. Tarski qui utilise essentiellement le premier théorème de Gödel suivant lequel la théorie ¹ introduite au chapitre 2 est essentiellement indécidable. Pour qu’une théorie mathématique T dans un langage 硫 soit indécidable, il suffit en effet de trouver un modèle 紐 de T dans lequel on puisse «définir» (en un sens à préciser) un modèle (en général la structure standard 麗N, +, x 礪 de l’arithmétique) d’une théorie essentiellement indécidable (principalement ¹). Ainsi, par exemple, la théorie des anneaux euclidiens, factoriels, commutatifs... est indécidable car, dans l’anneau Z, on peut définir (dans le langage des anneaux) la structure N. En effet, d’après le théorème de Lagrange suivant lequel tout nombre positif est somme de quatre carrés, on a, dans Z, l’équivalence:

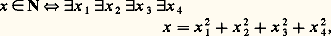dans laquelle le membre de droite est une formule du langage des anneaux, l’addition et la multiplication des entiers naturels étant définies par la restriction de l’addition et de la multiplication de Z aux éléments de Z vérifiant cette formule. On démontre ainsi de nombreux résultats: la théorie des relations binaires, la théorie des corps, la théorie des groupes, etc., sont indécidables (Par contre, la théorie des corps finis – c’est le théorème d’Ax et Kochen – et la théorie des groupes commutatifs sont des théories décidables.)

Les techniques utilisées pour démontrer la décidabilité d’une théorie mathématique ne relèvent pas, de la théorie des fonctions récursives et font appel en général à des résultats difficiles d’algèbre, d’arithmétique etc. (par exemple le théorème d’Ax et Kochen). Par contre, ces résultats sont intéressants à analyser du point de vue de la complexité des procédures de décision dont ils affirment l’existence. Or, il s’avère que toutes les théories décidables connues ont des procédures de décision qui peuvent demander, avant d’obtenir une réponse, un temps supérieur à l’âge de l’Univers! Autrement dit, l’espoir d’utiliser ces procédures de décision pour démontrer par ordinateur des théorèmes de mathématiques est, malgré l’existence de telles procédures, illusoire. Citons au hasard quelques résultats illustrant ce point de vue. Soit T size=1^戮 l’ensemble des formules écrites avec l’addition seulement et qui sont vraies dans N. Cet ensemble est décidable, mais on peut montrer que, pour tout programme de calcul de la fonction caractéristique de T size=1^戮, il existe une infinité de formules F telles que, si |F| désigne le nombre de symboles dont elle est constituée, il faudra que ce programme effectue au moins: 2² size=1^﨎.|F| (où 﨎 est un nombre positif) étapes de calcul avant de donner une réponse. Si on considère maintenant l’ensemble des formules écrites avec l’addition et la multiplication et qui sont vraies dans R, on a un résultat analogue, mais, dans ce cas, la borne inférieure est plus faible et égale à 2 﨎.|F| . Ainsi, bien que la théorie du premier ordre de l’addition et de la multiplication des réels soit décidable (théorème de A. Tarski), dès que l’on veut vérifier la vérité ou la fausseté d’une formule assez longue, les algorithmes de décision peuvent demander un nombre d’étapes ou un temps fabuleux.

5. Quelques exemples de généralisation et d’application de la récursivité

On peut étendre la notion de calcul par machine en introduisant la possibilité de «consulter un oracle». Par oracle, nous entendons ici un ensemble X d’entiers; permettre à la machine de consulter l’oracle X, c’est l’autoriser à poser la question «n 捻 X?» et à poursuivre son calcul selon la réponse qui lui est faite. On introduit, à cet effet, la notion de récursivité relative: on dira qu’un ensemble Y est récursif en X s’il existe une machine qui, en utilisant X comme oracle, décide, pour tout entier n , en un nombre fini de démarches, que n 捻 Y, ou pas. Le degré de Turing de X est l’ensemble de tous les Y tels que X est récursif en Y et Y est récursif en X.

En 1948, E. Post posait le problème suivant: Existe-t-il deux ensembles récursivement énumérables X et Y tels que X n’est pas récursif en Y et Y n’est pas récursif en X? R. M. Friedberg (1957) et A. A. Mu face="EU Caron" カnik (1956) ont apporté (indépendamment et par la même méthode!) une réponse positive à cette question. Pour ce faire, ils ont dû définir pas à pas, en une énumération récursive, deux ensembles X et Y de telle sorte que, pour toute machine de Turing M, si M munie de l’oracle X définit un ensemble X récursif en X, on ait Y X et vice versa. L’idée est d’attribuer un ordre de priorité aux différents moyens de satisfaire à ces exigences à partir d’approximations finies de X et de Y. Supposons que, à une étape de l’énumération, il faille, pour satisfaire par un moyen donné à une exigence donnée, renoncer à tel autre moyen mis en œuvre antérieurement pour satisfaire à une autre exigence: on tranche selon la priorité relative des deux moyens. Il faut alors prouver que toutes les exigences sont finalement satisfaites de façon définitive, ce qui demande, tant pour résoudre le problème de Post que pour réaliser d’autres constructions, une analyse combinatoire parfois très fine. Le procédé inventé par Friedberg et par Mu face="EU Caron" カnik, appelé métode de priorité a été brillamment exploité ultérieurement par de nombreux mathématiciens pour mettre en évidence l’extraordinaire richesse de la structure des degrés de Turing et pour opérer d’autres applications en récursivité. Notons aussi que cette technique a été utilisée récemment (1975) en théorie des ensembles par D. Martin pour démontrer que les jeux boréliens (cf. théorie axiomatique des ENSEMBLES) sont déterminés, ce qui nous conduit fort loin du problème de Post!

Théorie descriptive effective des ensembles

Les Borel, Lebesgue, Luzin et autres (ce qu’on appelle parfois l’école semi-intuitionniste), en élaborant la théorie descriptive (classique) des ensembles, avaient eu l’intuition de ses aspects effectifs. Dans les années cinquantes, S. C. Kleene jetait les fondements d’une théorie permettant de rendre compte rigoureusement de cette intuition. Le principal outil de l’analyse de Kleene est la théorie de la récursivité.

On prendra ici comme espace topologique de référence l’espace de Baire de toutes les fonctions de N dans N, que nous notons ^N. Ce que nous dirons s’applique également à la droite réelle R, à l’espace de Cantor 2^N et, en gros, à tout espace polonais.

L’espace de Baire ^N est muni d’une métrique naturelle: aussi, pour f g , posons d (f , g ) = (n + 1)^-1, où n est le premier entier tel que f (n ) g (n ). Pour cette métrique, l’espace ^N est complet. À chaque fonction h dont le domaine et l’image sont des parties finies de N, on associe un ouvert élémentaire 類 =g |g (n ) = h (n ) pour tout n dans le domaine de h . Les ouverts élémentaires forment une base dénombrable pour la topologie sur ^N.

La hiérarchie borélienne classique sur ^N mesure la complexité d’un ensemble X par le nombre de fois où il faut itérer les opérations de complément et réunion dénombrable pour obtenir X à partir des ouverts élémentaires: elle définit, pour tout ordinal 見 麗 尿¹, la classe ⁰ size=1^見, qui est l’ensemble des boréliens qui s’obtiennent en répétant au plus 見 fois ces opérations. Elle introduit, de plus, la classe duale:

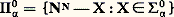et les classes ⁰ size=1^見 = 刺⁰ size=1^見 惡 ⁰ size=1^見.

À cette mesure de complexité de X par le plus petit 見 麗 尿¹, tel que X 捻 ⁰ size=1^見 聆 刺⁰ size=1^見, les logiciens, suivant S. C. Kleene, ont ajouté un second principe de classement, définissant ainsi la hiérarchie borélienne effective . Fixons une énumération naturelle k 料 N^k des ouverts élémentaires; nous disons q’un ensemble ouvert X est ⁰¹ si X est une réunion récursive d’ouverts élémentaires, c’est-à-dire si:

pour un ensemble récursif d’entiers R. On désigne la classe duale par 刺⁰¹ et 刺⁰¹ 惡 ⁰¹ par ⁰¹. En poursuivant ces définitions par récurrence simultanée sur 見 麗 尿¹, on obtient deux classes ⁰ size=1^見 et 刺⁰ size=1^見 dont les éléments sont indexés de façon naturelle par les entiers, et telles qu’un ensemble X est ⁰ size=1^見 si X est réunion d’ensembles appartenant à: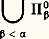

et si, de plus, cette réunion est récursive, compte tenu de l’indexation.

Plus généralement, si f 捻 ^N, les classes ⁰ size=1^見(f ) et 刺⁰ size=1^見(f ) sont définies de la même manière excepté qu’on remplaces les réunions récursives par les réunions récursives en f (voir, ci-dessus, Théorie de la complexité ) et l’on pose:

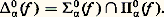Cette hiérarchie est beaucoup plus fine que la hiérarchie classique: en particulier:

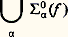est dénombrable, alors que, pour chaque 見 麗 尿¹, ⁰ size=1^{見 + 1 0} size=1^見 a la puissance du continu. Qui plus est, la hiérarchie ⁰ size=1^見(f ) est close bien avant 尿¹. Soit 諸^1(f) le premier ordinal qui n’est pas isomorphe à un bon ordre récursif en f sur les entiers; alors:

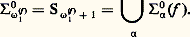Cependant, quel que soit 見 麗 尿¹, on a:

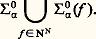La classe des ensembles analytiques , notée ¹¹, est définie comme la famille de toutes les parties de ^N qui sont l’image par une fonction continue d’un ensemble borélien; la classe duale est notée 刺¹¹ et ¹¹ = 刺¹¹ 惡 ¹¹. Souslin a démontré en 1916 que ¹¹ 刺¹¹ mais que:

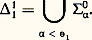Disons qu’un ensemble X est ¹¹(f ) si X est l’image par une fonction récursive en f d’un ensemble ⁰ size=1^見(f ). Alors, tout ensemble ¹¹ est de la forme ¹¹(f ), et la version effective du résultat de Souslin est que:

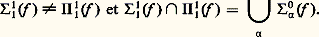Notons que cette version est beaucoup plus fine que le résultat initial puisque, en particulier:

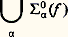est une famille dénombrable, alors que:

a la puissance du continu. Les principaux théorèmes de la théorie descriptive classique sur les ensembles analytiques et boréliens ont reçu une version effective. Longtemps, ces raffinements effectifs n’ont pas eu d’applications en dehors de la logique; mais il apparaît maintenant des résultats utiles aux autres mathématiciens, dont les démonstrations se servent de la théorie effective et ne risquent guère d’être intelligibles sans elle.

Récursivité et ensembles admissibles

La famille des ensembles héréditairement finis comprend les ensembles finis entiers, les ensembles finis de ceux-ci, etc., indéfiniment; nous désignons cette famille par HF. Plus précisément, on pose: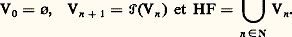

Il est clair que les éléments d’un élément de HF sont eux-mêmes des éléments de HF: on dit que HF est un ensemble transitif . Un premier lien entre la récursivité et la théorie des ensembles résulte d’une comparaison entre deux sortes d’ensembles d’entiers: d’une part, les ensembles récursifs et récursivement énumérables et, d’autre part, ceux qui sont définissables dans la structure (HF, face=F0019 捻 | HF) où, de manière générale, 捻 | X désigne la restriction de la relation 捻 à X. Pour préciser, considérons le langage (face=F0019 捻, =) de la théorie des ensembles; une formule est dite ⁰ si tous ses quantificateurs sont bornés, c’est-à-dire s’ils sont de la forme 說 u 捻 ^v ou 葉 u 捻 ^v. On appelle formule ¹ celles qui s’obtiennent à partir de formules ⁰ au moyen d’une quantification existentielle.

Soit A un ensemble transitif et X une partie de A. On dit que X est ¹ dans A si X est définissable dans la structure (A, face=F0019 捻 | A) par une formule ¹ à paramètres dans A et que X est dans A si X et A 漣 X sont ¹ dans A.

La comparaison que nous avons évoquée plus haut est la suivante: La théorie de la récursivité sur N s’identifie exactement avec la théorie de la définissabilité dans HF aux niveaux et ¹; les ensembles récursifs sont ceux qui sont dans HF, les ensembles récursivement énumérables sont ceux qui sont ¹ dans HF. Cela conduit à une généralisation infinitaire de la récursivité: au lieu de HF, on introduit un autre ensemble transitif A et l’on considère, pour X 說 A, que X est récursivement énumérable au sens de A , ce que l’on écrit «X est A-r.e.», si X est ¹ dans A, que X est récursif au sens de A si X est dans A, et enfin (élément essentiel dans la réussite de cette généralisation) que X est fini au sens de A si X 捻 A. Bien entendu, cela ne conduit pas à une bonne généralisation de la récursivité classique pour tout ensemble A, mais S. Kripke et R. Platek ont découvert (1964-1966) un ensemble d’axiomes, qu’on appelle KP, et ont montré que, pour tout ensemble transitif A, si (A, face=F0019 捻 | A) est un modèle de KP, cette généralisation de la récursivité au sens de A reste pour l’essentiel justiciable de l’intuition et des méthodes relatives aux processus effectifs. En gros, on peut dire que KP est la sous-théorie de ZF (cf. LOGIQUE MATHÉMATIQUE - Théorie des ensembles) obtenue en supprimant l’axiome de l’ensemble des parties et en restreignant les schémas de compréhension et de remplacement aux formule . On appelle admissible un ensemble transitif modèle de KP. Le transfert des résultats de base de la récursivité classique au cas admissible a été réussi jusqu’à l’étude des degrés de Turing et la solution, dans maints cas importants, du problème de Post.

Théorie des modèles et langages infinitaires

Les formules usuelles d’un langage du premier ordre sont des objets finis, avec une syntaxe ou grammaire récursive, et leur notion de validité est récursivement énumérable, ce dernier fait étant une conséquence du théorème de complétude. Pour tout ensemble admissible dénombrable A, nous allons définir une extension de 硫, notée 硫^A, dont les formules seront des objets A-finis ayant une syntaxe A-récursive tandis que la notion de validité sera A-récursivement énumérable. Pour définir les langages 硫^A plus simplement, nous introduisons d’abord le langage 硫 諸|, 諸 qui est la réunion de tous les 硫^A quand A parcourt les ensembles admissibles dénombrables. Historiquement, 硫 諸|, 諸 a été étudié avant l’introduction des sous-langages 硫^A, de même que la hiérarchie borélienne classique a précédé la version effective, et les langages 硫^A raffinent 硫 諸|, 諸 de la même manière que les classes ⁰ size=1^見(f ) raffinent ⁰ size=1^見. Les formules de 硫 諸|, 諸 sont définies par les mêmes clauses inductives que les formules de 硫, excepté pour la conjonction et la disjonction où l’on convient de ceci: si 淋 est un ensemble dénombrable de formules de 硫 諸|, 諸 alors la conjonction et la disjonction des formules de 淋, notées 廬廬 淋 et 鈴鈴 淋 ou:

sont encore des formules de 硫 諸|, 諸. Alors 硫^A est défini comme 硫 諸|, 諸 惡 A; ce qui revient à se restreindre à des conjonctions et à des disjonctions A-finies: face=F0019 廬廬 淋 et 鈴鈴 淋 sont dans 硫^A seulement quand 淋 捻 A.

L’utilité de ces langages 硫^A, appelés langages admissibles , vient au premier chef de ce qu’il vérifient des formes du théorème de compacité et du théorème de complétude (cf. LOGIQUE MATHÉMATIQUE - Théorie des modèles). De façon précise:

Théorème de Barwise (1969). Soit T un ensemble A-récursivement énumérable de formules de 硫^A, alors:

– si 﨏 捻 硫^A est une conséquence de T, il existe un sous-ensemble A-fini T de T tel que 﨏 est déjà conséquence de T .

– l’ensemble des formules 硫^A qui sont des conséquences de T est A-récursivement énumérable.

En même temps qu’une généralisation de la théorie des modèles usuelle, l’étude de 硫 諸|, 諸 et de ses sous-langages 硫^A présente un lien étroit avec celle des ensembles boréliens et analytiques; à la base de cette liaison, il y a le résultat suivant: Pour g 捻 ^N, notons M^g la structure ayant N pour domaine et l’égalité, la fonction successeur et g pour relations et fonctions de base. Soit 硫 le langage de cette structure. Définisson Hyp(f ) comme l’intersection de tous les ensembles admissibles contenant f comme élément. Alors Hyp(f ) est un ensemble admissible et, pour qu’une partie X de ^N soit ¹¹(f ), il faut et il suffit qu’il existe une formule 切 de 硫^Hyp(f ) telle que l’on ait:

pour tout g 捻 ^N. Partant de ce résultat, on peut retraduire, redémontrer et généraliser dans le cadre de la théorie des modèles la plupart des résultats de base sur les ensembles ¹¹(f ) et ¹¹(f ).

récursivité [ rekyrsivite ] n. f.

• 1968; de récursif

♦ Didact. Caractère de ce qui est récursif.

● récursivité nom féminin (de récursif) Propriété que possède une règle ou un élément constituant de pouvoir se répéter de manière théoriquement indéfinie. (C'est une propriété essentielle des règles d'une grammaire générative, celle qui permet d'engendrer un nombre infini de phrases.) Qualité d'un programme informatique récursif. Théorie destinée à fournir un cadre rigoureux à l'étude des notions intuitives de calculabilité et de décidabilité effectives. (Church a montré [1936] que la récursivité est l'équivalent mathématique de la calculabilité effective : la fonction récursive est une fonction rigoureusement calculable.)

récursivité [ʀekyʀsivite] n. f.

ÉTYM. V. 1968; de récursif.

❖

♦ Didact. Caractère de ce qui est récursif. || Récursivité d'une règle, d'un programme.

Encyclopédie Universelle. 2012.